RAZÓN O RELACIÓN de
dos cantidades es el resultado de comparar dos cantidades.
Dos cantidades pueden compararse de dos maneras:
Hallando en cuánto excede una a la otra, es decir, restándolas, o hallando
cuántas veces contiene una a la otra, es decir, dividiéndolas. De aquí que haya
dos clases de razones: razón aritmética o diferencia y razón geométrica o por
cociente.
RAZÓN ARITMÉTICA O POR DIFERENCIA de dos cantidades es la diferencia indicada de dichas cantidades.
Las razones aritméticas se pueden escribir de dos
modos: separando las dos cantidades con el signo – o con un punto (.).
Así, la razón aritmética de 6 a 4 se escribe: 6 – 4
ó 6. 4 y se lee seis es a cuatro.
RAZÓN GEOMÉTRICA O POR COCIENTE de dos cantidades es el cociente indicado de dichas cantidades.
Las razones geométricas se pueden escribir de dos
modos: en forma de quebrados, separados numerador y denominador por una raya
horizontal o separadas las cantidades por el signo de división.
Así, la razón geométrica de 8 a 4 se escribe u 8 4,
y se lee, ocho es a cuatro.
Los términos de la razón geométrica se llaman
antecedente el primero y consecuente el segundo. Así, en la razón 8 4, el antecedente es 8 y el consecuente 4.
PROPIEDADES DE LAS
RAZONES ARITMÉTICAS O POR DIFERENCIAS
Como la razón aritmética o por diferencia de dos
cantidades no es más que la diferencia indicada de dichas cantidades, las
propiedades de las razones aritméticas serán las propiedades de toda resta o
diferencia:
1. Si
al antecedente de una razón aritmética se suma o resta un número, la razón
queda aumentada o disminuida en ese número.
2. Si
al consecuente de una razón aritmética se suma o resta un número, la razón
queda disminuida en el primer caso y aumentada en el segundo en el mismo
número.
3. Si
al antecedente y consecuente de una razón aritmética se suma o resta un mismo
número, la razón no varia.
PROPIEDADES DE LAS RAZONES GEOMÉTRICAS O POR
COCIENTE
Como la razón geométrica o por cociente de dos
cantidades no es más que una división indicada o un quebrado, las propiedades
de las razones geométricas serán las propiedades de los quebrados:
1. Si
el antecedente de una razón geométrica se multiplica o divide por un número, la
razón queda multiplicada o dividida por ese número.
2. Si
el consecuente de una razón geométrica se multiplica o divide por un número, la
razón queda dividida en el primer caso y multiplicada en el segundo por ese
mismo número.
3. Si
el antecedente y el consecuente de una razón geométrica se multiplican o
dividen por un mismo número, la razón no varía.
(En los ejercicios siguientes, cuando se diga
simplemente razón o relación, se entenderá que la razón pedida es geométrica).
1. Cite
dos números cuya razón aritmética sea 6; dos números cuya razón geométrica sea .
2. Hallar
la razón aritmética y geométrica de :
3. a)
60 y 12. R. 48; 5. c) 5.6 y 3.5 R. 2.1; .
4. Hallar
la relación entre las edades de dos niños 10 y 14 años. R. .
5. Cite
tres pares de números que estén en la relación de 2 y 3.
6. Cite
tres pares de números cuya razón sea ; tres pares de
números cuya relación sea de 1 a 6.
7. La
razón de dos números es . Si el menor es 20, ¿
cuál es el mayor? R. 24.
8. El
mayor de dos números es 42 y la relación entre ambos de 5 a 7. Hallar el número
menor. R 30.
9. Dos
números son entre sí como 2 es a 17. Si el menor es 14, ¿cuál es el mayor? R.
119.
PROPORCIONES
ARITMÉTICAS.
EQUIDIFERENCIA O PROPORCIÓN ARITMÉTICA es la igualdad de dos diferencias o razones
aritméticas.
Una equidiferencia se escribe de los dos modos
siguientes:
a – b = c – d y a . b :: c . d y se lee a es a b
como c es a d.
TÉRMINOS DE UNA EQUIDIFERENCIA
Los términos de una equidiferencia se llaman: extremos
el primero y el cuarto, y medios el segundo y el tercero. También según lo
visto antes se llaman antecedentes al primero y tercer términos y consecuentes
al segundo y al cuarto.
Así, en la diferencia 20 – 5 = 21 – 6, 20 y 6 son
los extremos, y 5 y 21 son los medios, 20 y 21 son los antecedentes, 5 y 6 son
los consecuentes.
CLASES DE EQUIDIFERENCIAS
Hay dos clases: Equidiferencia discreta, que es
aquella cuyos medios no son iguales, por ejemplo, 9 – 7 = 8 – 6 y
equidiferencia contínua, que es la que tiene los medios iguales; por ejemplo,
10 – 8 = 8 – 6.
PROPIEDAD FUNDAMENTAL DE LAS EQUIDIFERENCIAS
En toda equidiferencia la suma de los extremos es
igual a la suma de los medios.
Sea la equidiferencia a – b = c – d. Vamos a
demostrar que a + d = c + b.
En efecto: sumando a los dos miembros de la
equidiferencia dada a- - b = c – d un extremo y un medio, b + d, tendremos: a –
b + b + d = c – d + b + d y simplificando, queda a + d = c + b que era lo que
queríamos demostrar.
En la equidiferencia 8 – 6 = 9 – 7 tenemos: 8 + 7 =
9 + 6 o sea 15 = 15.
De la propiedad fundamental de las equidiferencias
se derivan los siguientes corolarios:
1. En
toda equidiferencia un extremo es igual a la suma de los medios, menos el otro
extremo.
2. Sea
la equidiferencia a – b = c – d. Vamos a demostrar que a = b + c – d.
En efecto: ya sabemos
por la propiedad fundamental, que: a + d = b + c.
Restando d a ambos
miembros, tendremos: a + d – d = b + c – d y simplificando a = b + c – d.
En 9 – 5 = 10 – 6 tenemos
que 9 = 5 + 10 – 6.
3. En
toda equidiferencia un medio es igual a la suma de los extremos, menos el otro
medio.
Sea la equidiferencia a – b = c – d. Vamos a
demostrar que b = a + d – c.
En efecto: ya sabemos que a + d = b + c.
Restando c a los dos miembros, tendremos: a + b – c
= b + c – c y simplificando b = a + d – c.
En 11 – 7 = 9 – 5 tenemos que 7 = 11 + 5 – 9.
MEDIA DIFERENCIA O MEDIA ARITMÉTICA es cada uno de los términos medios de una
equidiferencia continua, o sea cada uno de los medios de una equidiferencia,
cuando son iguales. Así, en la equidiferencia 8 – 6 = 6 – 4, la media
diferencial es 6.
La media diferencial es igual a la semisuma de los
extremos.
Sea la equidiferencia a – b = b – c. Vamos a
demostrar que
En efecto: por la propiedad fundamental sabemos que
a + c = b + b o sea a + c = 2b.
Dividiendo ambos miembros por 2 queda: o
sea = b que era lo que
queríamos demostrar.
En 12 – 9 = 9 – 6 tenemos 9 = .
HALLAR TÉRMINOS DESCONOCIDOS EN EQUIDIFERENCIAS
1. Hallar
el término desconocido en 8 – 6 = 4 – x.
2. Como
el término desconocido es un extremo y un extremo es igual a la suma de los
medios menos el extremo conocido, tendremos:
Y queda, sustituyendo
el valor de x en la equidiferencia: 8 – 6 = 4 – 2.
2) Hallar el término
desconocido en 3.4 – x = - 1.
Como el término
desconocido es un medio y un medio es igual a la suma de los extremos menos el
medio conocido, tendremos:
y sustituyendo el
valor de x: 3.4 - 2 - 1.
3. Hallar
el término desconocido en 14 – x = x – 3.04
Aquí el término desconocido es la media
diferencial, que es igual a la semisuma de los extremos, luego:
y queda, sustituyendo el valor de x en la
equidiferencia dada:
HALLAR EL TÉRMINO MEDIO DIFERENCIAL ENTRE DOS
NÚMEROS
Hallar la media diferencial entre 8.04 y 4
No hay más que formar una equidiferencia continua
cuyo medio diferencial sea x y los extremos los números dados y despejar x;
Y sustituyendo el valor de x: 8.04 – 6.02 = 6.02 –
4
PROPORCIÓN GEOMÉTRICA o EQUICOCIENTE es la igualdad de dos razones geométricas o por
cociente.
Una proporción geométrica se escribe de los dos
modos siguientes:
y se lee: a es a b como c es a d.
TÉRMINOS DE UNA PROPORCIÓN GEOMÉTRICA
Los términos de una proporción geométrica se
llaman: extremos el primero y el cuarto, y medios el segundo y tercero.
También, según lo visto antes, se llaman
antecedentes el primero y el tercer términos, y consecuentes el segundo y
cuarto términos.
Así, en la proporción los
extremos son 8 y 5, y los medios 10 y 4; los antecedentes son 8 y 10, y los
consecuentes 4 y 5.
CLASES DE PROPORCIONES GEOMÉTRICAS
Hay dos clases de proporciones geométricas:
Proporción discreta, que es aquella cuyos medios no son iguales; por ejemplo, 8
: 4 :: 10 : 5, y proporción continua, que es la que tiene los medios iguales; por
ejemplo, 20 : 10 :: 10 : 5.
PROPIEDAD FUNDAMENTAL DE LAS PROPORCIONES
GEOMÉTRICAS TEOREMA
En toda proporción geométrica el producto de los
extremos es igual al producto de los medios.
Sea la proporción . Vamos a demostrar
que a d = c b.
En efecto: multiplicando ambos miembros de la
igualdad por
el producto de un medio y un extremo, b x d, para lo cual basta multiplicar
solamente los numeradores, tendremos:
Y simplificando queda: a x d = c x b que era lo que
queríamos demostrar.
En la proporción tenemos
que 6 x 2 = 3 x 4 o sea 12 = 12
De la propiedad fundamental de las proporciones
geométricas se derivan los siguientes corolarios:
1. En
toda proporción geométrica un extremo es igual al producto de los medios
divididos por el otro extremo.
Sea la proporción Vamos a demostrar
que a =
En efecto: ya sabemos por la propiedad fundamental
que a x d = b x c. Dividiendo los dos miembros de esta igualdad por d,
tendremos:
2) En toda proporción geométrica un medio es igual
al producto de los extremos dividido por el otro medio.Sea la proporción
En efecto: Ya sabemos
que ad = bc.
Dividiendo ambos miembros de esta igualdad por c
tendremos:
MEDIA PROPORCIONAL O MEDIA GEOMÉTRICA es cada uno de los términos medios de una
proporción geométrica continua, o sea, cada uno de los términos medios de una
proporción geométrica, cuando son iguales. Así, en la proporción 8:4::4:2 la
media proporcional es 4.
La media proporcional es igual a la raíz cuadrada
del producto de los extremos.
Sea la proporción continua vamos
a demostrar que
En efecto: ya sabemos por la propiedad fundamental
que ac=bb, o
sea, ac=b2.
Extrayendo la raíz cuadrada a ambos miembros,
tenemos:
Y simplificando: que
era lo que queríamos demostrar.
HALLAR TÉRMINOS DESCONOCIDOS EN PROPORCIONES
GEOMÉTRICAS
1. Hallar
el término desconocido en 8:4::10:x.
2. Como
el término desconocido es un extremo y un extremo es igual al producto de los
medios dividido por el extremo conocido, tendremos:
. Sustituyendo el
valor de la x en la proporción dada, queda: 8:4::10:5.
3. Hallar
el término desconocido en 10:1/6::x:4.
4. Como
el término desconocido es un medio y un medio es igual al producto de los
extremos dividido por el medio conocido tendremos:
Sustituyendo
el valor de x en la proporción dada queda. 10:1/6::240:4.
5. Hallar
el término desconocido en 25:x::x.1/6.
Como el término desconocido es la media
proporcional y la media proporcional es la raíz cuadrada del producto de los
extremos, tendremos:
Sustituyendo el valor de x en la proporción dada,
queda:
Hallar
el término desconocido en:
|
Resultados
|
8 : x
:: 16 : 4
|
2
|
X : 1/5
:: 6 : 2
|
3/5
|
x:0.04
:: 24 : 0.4
|
2.4
|
5: ½ ::
x : 0.04
|
0.4.
|
14.25:
14 :: x : 0.002
|
57/28000
|
1/3:2/5::4.25:x
|
5 1/10.
|
0.04:
0.05 :: 0.06: x
|
0.075
|
8 ¼: 5
1/6 :: x: 3 1/7.
|
5 4/217
|
1/3:1/5::x:2/3
|
1 1/9
|
0.03:x::1/6:2/9
|
1/25
|
5
2/3:x::8 ¼:5/6
|
170/297
|
16:x::x:25
|
20
|
1/12:3
1/6::2/3:x
|
25 1/3
|
0.49:x::x:
0.64
|
0.56
|
0.45:1/12::10
2/9:x
|
1
217/243
|
¼:x::x:9/16
|
3/8
|
3.45:1/8::x:4.36
|
120.336
|
2.25:x::x:1.69
|
1.95
|
HALLAR EL TÉRMINO MEDIO PROPORCIONAL ENTRE DOS
NÚMEROS
Hallar el término medio proporcional entre 16 y 81.
No hay más que formar una proporción geométrica
continua cuyo medio proporcional sea x y los extremos los números dados y
despejar x. 16:x::x:81,
Sustituyendo el valor de x en la proporción dada,
queda: 16:36::36:81.
Hallar el término medio proporcional entre:
|
Solución
|
81 y 4.
|
18
|
¼ y
1/9.
|
1/6
|
64 y
25.
|
40
|
25/36 y
40/81
|
35/54
|
49 y
0.25.
|
3.5
|
0.0144
y 1/324
|
1/150
|
0.16. y
169
|
5.2
|
121/169
y 289/361.
|
187/247
|
0.0064
y 225
|
1.2
|
2 ¼ y 3
1/16.
|
2 5/8
|
144 y
0.0169
|
1.56
|
1
47/529 y 1 49/576.
|
1 2/23.
|
HALLAR UNA CUARTA PROPORCIONAL DE TRES NÚMEROS.
Cuarta proporcional es cualquiera de los cuatro
términos de una proporción geométrica discreta. Así, en la proporción
8:16::5:10, cualquiera de estos cuatro términos es cuarta proporcional respecto
de los otros tres.
Hallar una cuarta proporcional de 20, 1/3 y 2/5.
Se forma una proporción geométrica con estas tres
cantidades, poniendo de último extremo x y se despeja el valor de x:
20:1/3::2/5:x.
Sustituyendo el valor de x: 20:1/3::2/5:1/150.
Hallar el término medio proporcional entre:
|
Solución
|
5, 6, y
0.04.
|
0.04
|
150, 24
1/7 y 16 2/5
|
2
1679/2625.
|
5/6, ¼
y 2/3.
|
1/5
|
5/12,
0.004 y 3.24.
|
486/15625
|
1/16, 5
2/3 y 6 1/12
|
551 5/9
|
1/14,
5.34 y 16 2/5.
|
1226
8/125.
|
HALLAR UNA TERCERA PROPORCIONAL DE DOS NÚMEROS
Tercera o tercia proporcional es el primero o
cuarto término de una proporción geométrica continua. Así, en la proporción
20:10::10:5. 20 es una tercia proporcional de 10 y 5, y 5 es una tercia
proporcional de 20 y 10.
Hallar una tercera proporcional entre 1/5 y 6.
Se forma una proporción continua, poniendo de
término medio proporcional uno de los números dados y x de último extremo y se
despeja x:
Sustituyendo el valor de x: 1/5 : 6 :: 180.
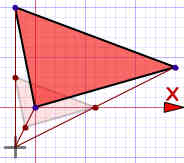
 . Sea X un elemento (visto como un punto) de E.
. Sea X un elemento (visto como un punto) de E. envía un punto M del espacio vectorial sobre el
envía un punto M del espacio vectorial sobre el . Sea X un elemento (visto como un punto) de E.
. Sea X un elemento (visto como un punto) de E. envía un punto M del espacio vectorial sobre el
envía un punto M del espacio vectorial sobre el ,
,  y
y  .
. ,
,  y
y  .
. a B
a B  (cuandoes:
(cuandoes:  o
o 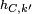 =
=  .
.


